Not Taylor, but Cordic

There are certain "Wow" moments in the education of a mathematics student. For me, they include Cantor's discovery of different levels of infinity, Gödel's Incompleteness Theorem, and the Lancaster War Model. But on most student's list will be the Taylor Series.

 Geometry and Arithmetic

To see that a geometric quantity (the sine of an angle of a right triangle), the ratio of two lengths, can be calculated with an arithmetic formula is astounding. And to implement this formula with only a few lines of computer code boggles. It is then tempting to assume that this is how your calculator does its calculations. And it probably would be except for one fact; your calculator is dumb.

Addition is easy, Multiplication is Hard

Since a calculator at its core uses binary arithmetic, it can easily do addition. You probably learned how to do it grade school. But multiplication is harder, with one exception. It is easy to multiply by 2 (10 in binary). Let's look at a simple example, 5 x 2 = 10. In binary, it is 101 x 10 = 1010. To multiply a binary number by 2, all you need do is shift the digits to the left, and shifting bits is very easy for a calculator's CPU to do.

The problem with using the Taylor series is that calculating just the first 5 terms of the sine expansion requires more than 50 multiplications and divisions. However, there are other ways of calculating the sine of an angle that, while harder for humans to do, are easier for computers.

COordinate Rotation DIgital Computer

An alternate method of calculating sine (and other transcendental functions) was developed in the 1960's that uses multiplications and divisions by 2. The details are beyond the scope of this post but can be found using the links below. At its heart is the decomposition of the angle into the sum of a set of specific angles.

Going from one angle to another is thought of as a rotation in space. The angles are picked so that the rotations are easy for the computer to sequence and calculate with. While the CORDIC algorithm was developed for early binary computers with limited core functionality, it has been adapted for calculators as evidenced with this from Texas Instruments

 Past threads on Graph-TI asked about the internal methods
     used to compute trigonometric and other transcendental functions.
     We wanted to add some specific information to this dialog so that
     someone could perhaps develop a short module for the classroom if
     they would like.  This topic should be interesting for background
     on calculators or as a good example of a math application.

     Most practical algorithms in use for transcendental functions
     are either polynomial approximations or the CORDIC method.  TI
     calculators have almost always used CORDIC, the exceptions being
     the CC-40, TI-74 and TI-95 which used polynomial approximations.
     In the PC world, the popular Intel math coprocessors like the
     8087 use CORDIC methods, while the Cyrix 83D87 uses polynomial
     methods.  There are pros and cons to both methods.

The details of CORDIC can be found at various sites with a few below. 

Links

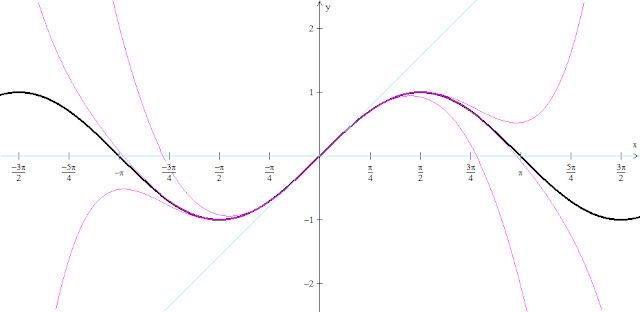
A paper on the CORDIC algorithm for the general student (from the site that hosts WinPlot which was used to generate the opening graphic)
http://math.exeter.edu/rparris/documents.html
http://math.exeter.edu/rparris/winplot.html
Sadly, Mr. Parris passed away a few years ago.  The school recently de-activated his account.  The paper can now be found here.

A paper from the Texas Instruments Calculator division about how their calculators use CORDIC
ftp://ftp.ti.com/pub/graph-ti/calc-apps/info/cordic.txt

How CORDIC was implemented on the HP-35 with details on the bit-shifting operation
http://www.jacques-laporte.org/Trigonometry.htm

The ubiquitous Wikipedia entry
http://en.wikipedia.org/wiki/CORDIC