
The probability of winning the PowerBall multi-state lottery with a single ticket is 1 in 292 million. In another post, I describe a way of visualizing these odds. But what if you played 175 million times? Your sure to win, right? You would if you could buy tickets for all 292 million possible number combinations, which would require you to have more than 500 Lottery terminals printing out one ticket a second for the 4 days between drawings. Oh, and you would need $400M to pay for them.
I'll just play for 292 million weeks
I know I am going to live forever, or at least 292 million weeks, so if I play one ticket a week, I have got to win at least once. Let's figure it out.
As with many probability questions, it will be easier to calculate the probability of not ever winning. Since it is possible to win more than once, you would have to calculate the probability of winning exactly once and losing all the other times, then of winning exactly twice (and losing all the other times), and so on.
The probability of winning with just one ticket is 1/n (I will use n instead of 292,000,000 from now on), and so the probability of not winning is (1-1/n).
The probability of not winning two weeks in a row is then (1-1/n)*(1-1/n), of not winning after three weeks is (1-1/n)^3, and of not winning n weeks in a row is (1-1/n)^n.
When I try to use my calculator to figure out the above for n=292,000,000, it breaks. However, I remember something from my calculus courses.
The probability of not winning two weeks in a row is then (1-1/n)*(1-1/n), of not winning after three weeks is (1-1/n)^3, and of not winning n weeks in a row is (1-1/n)^n.
When I try to use my calculator to figure out the above for n=292,000,000, it breaks. However, I remember something from my calculus courses.
So, when n=292,000,000, (1-1/n)^n is very close to 1/e.
Since the probability of not ever winning the PowerBall after playing 292 million times is close to 1/e, the probability of winning at least once is 1-1/e or about 63%. So even if you play that many times, you still have about a 1 in 3 chance of never winning the big prize.

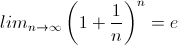
.gif)
No comments:
Post a Comment